Controle A
Exercice 1
1
Soient les points \(A (-1;-2)\), \(B (9;-3)\), \(C (1;2)\) et \(D (7;1)\). Les droites \((AB)\) et \((CD)\) sont-elles parallèles ?
2
Soient \(A (-2;-3)\), \(B (8;1)\), \(C (3;-1)\). Les points sont-ils alignés ?
Exercice 2
Dans un carré de côté 8, on a découpé deux triangles rectangles et deux trapèzes. A l'aide des 4 pièces, on reconstruit un rectangle. 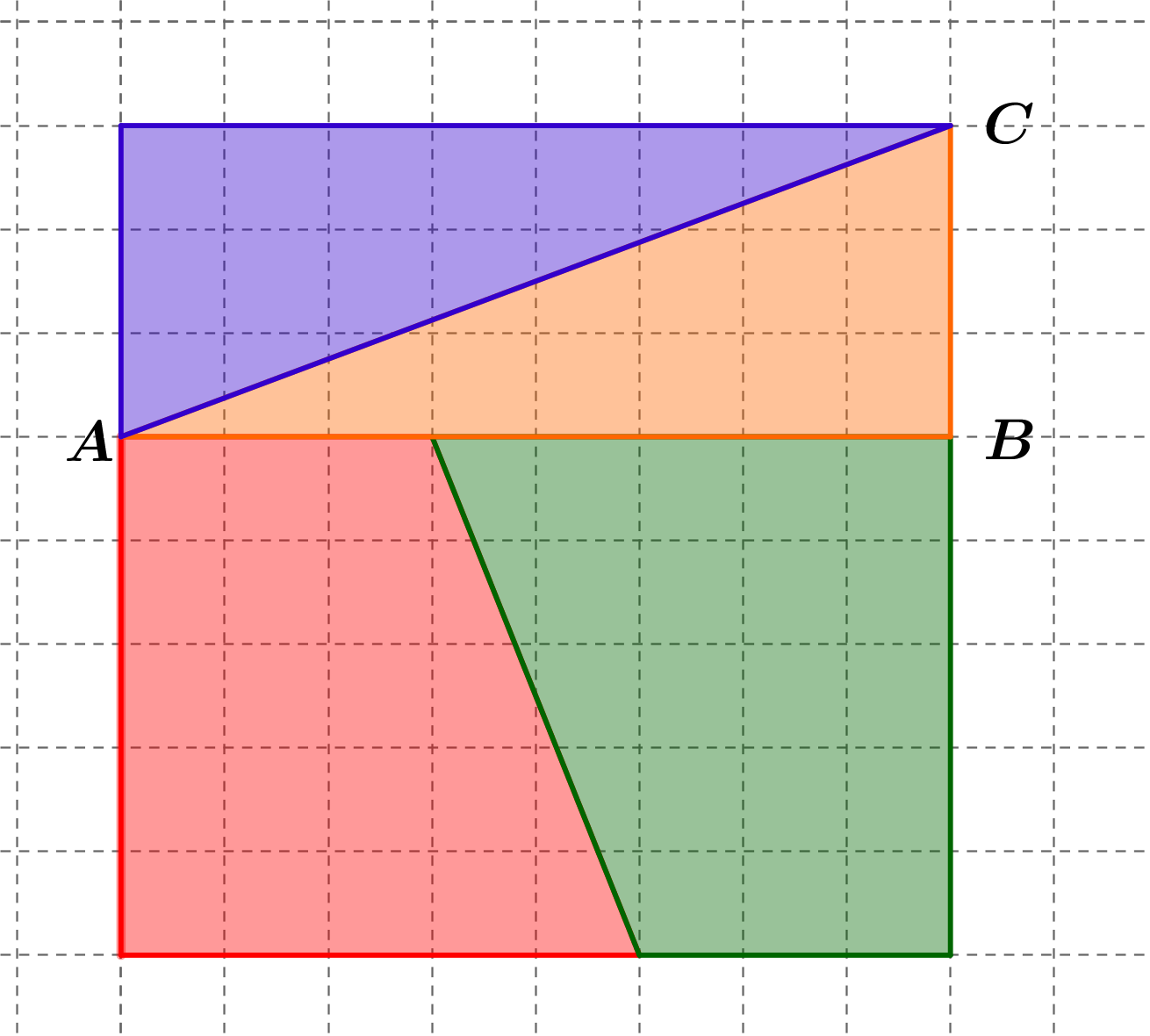
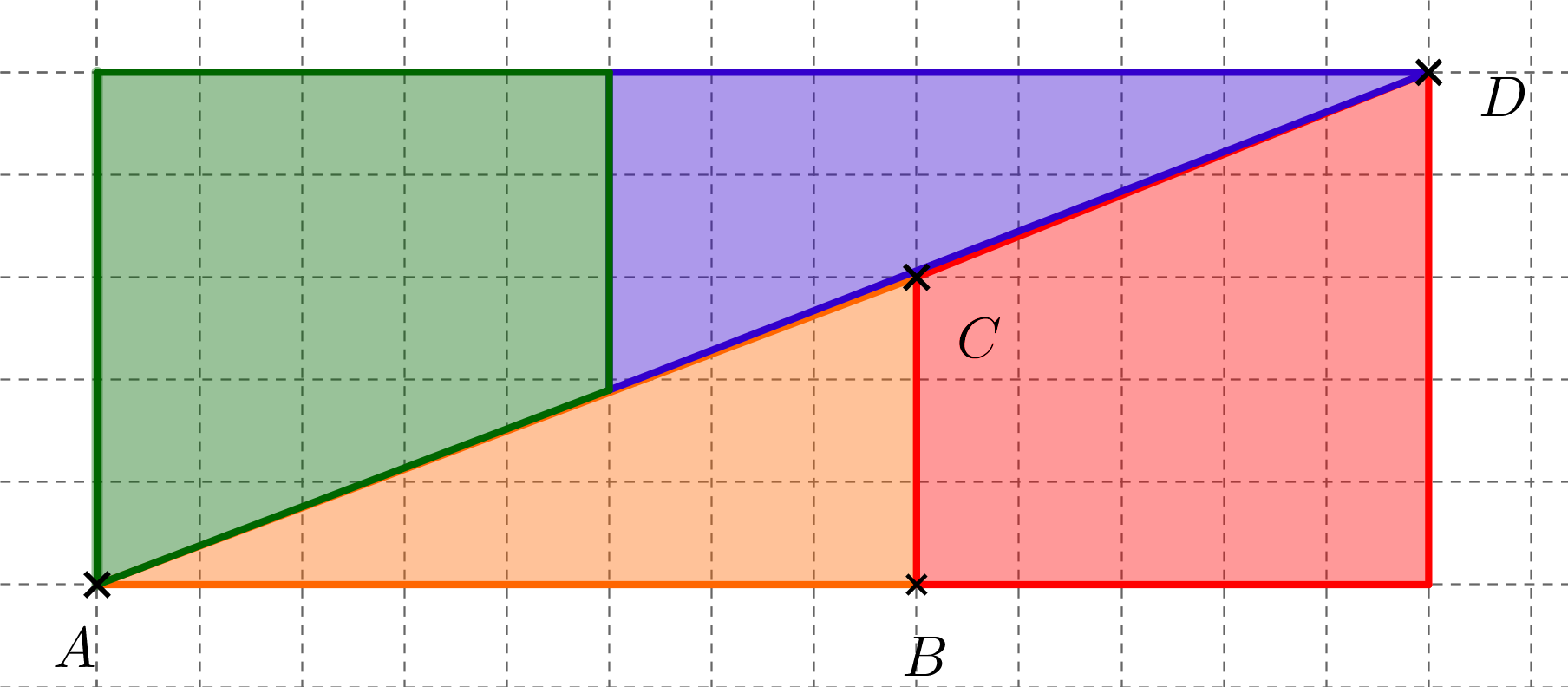


1
Quel problème constate-t-on au niveau des aires ?
2
Démontrer que les vecteurs \(\vec{AC}\) et \(\vec{CD}\) ne sont pas colinéaires dans la deuxième figure.
3
Expliquer l'observation faite à la question 1.
Exercice 3
Dans un repère, on donne les points \(A (0;2)\), \(B (-1;2)\), \(C (2;3)\). Soit \(E\) le point tel que \(\vec{BE} = \frac{5}{2} \vec{BA} + \frac{3}{2} \vec{AC}\)
1
Faire une figure.
2
On écrit les coordonnées de \(E (x_E;y_E)\). En calculant les coordonnées de \(\vec{BE}\) et \(\frac{5}{2} \vec{BA} + \frac{3}{2} \vec{AC}\), déterminer les coordonnées de \(E\).
3
Emettre une conjecture pour les droites \((AE)\) et \((BC)\) puis la démontrer.
Exercice 4
Soient \(A,B,C\) trois points formant un triangle quelconque. Soient \(M\) et \(N\) tels que : $$ \vec{AM} = \frac{1}{3} \vec{AB} \text{ et } \vec{AN} = \frac{1}{3} \vec{AC} $$
\(I\) est le milieu du segment \([MN]\) et \(J\) est le milieu du segment \([BC]\).
En utilisant la méthode de votre choix, démontrez que les points \(A\), \(I\) et \(J\) sont alignés (on pourra se placer dans un repère bien choisi parmi les points donnés, ou utiliser la relation de Chasles).Controle B
Exercice 1
1
Soient les points \(A (-1;-2)\), \(C (1;2)\), \(D (7;1)\) et \(E (4;-5)\). Les droites \((AC)\) et \((DE)\) sont-elles parallèles ?
2
Soient \(A (-2;1)\), \(B (4;-2)\), \(C (8;-4)\). Les points sont-ils alignés ?
Exercice 2
On a découpé ci-dessous le triangle en 4 pièces qu'on a réassemblé différemment en dessous. 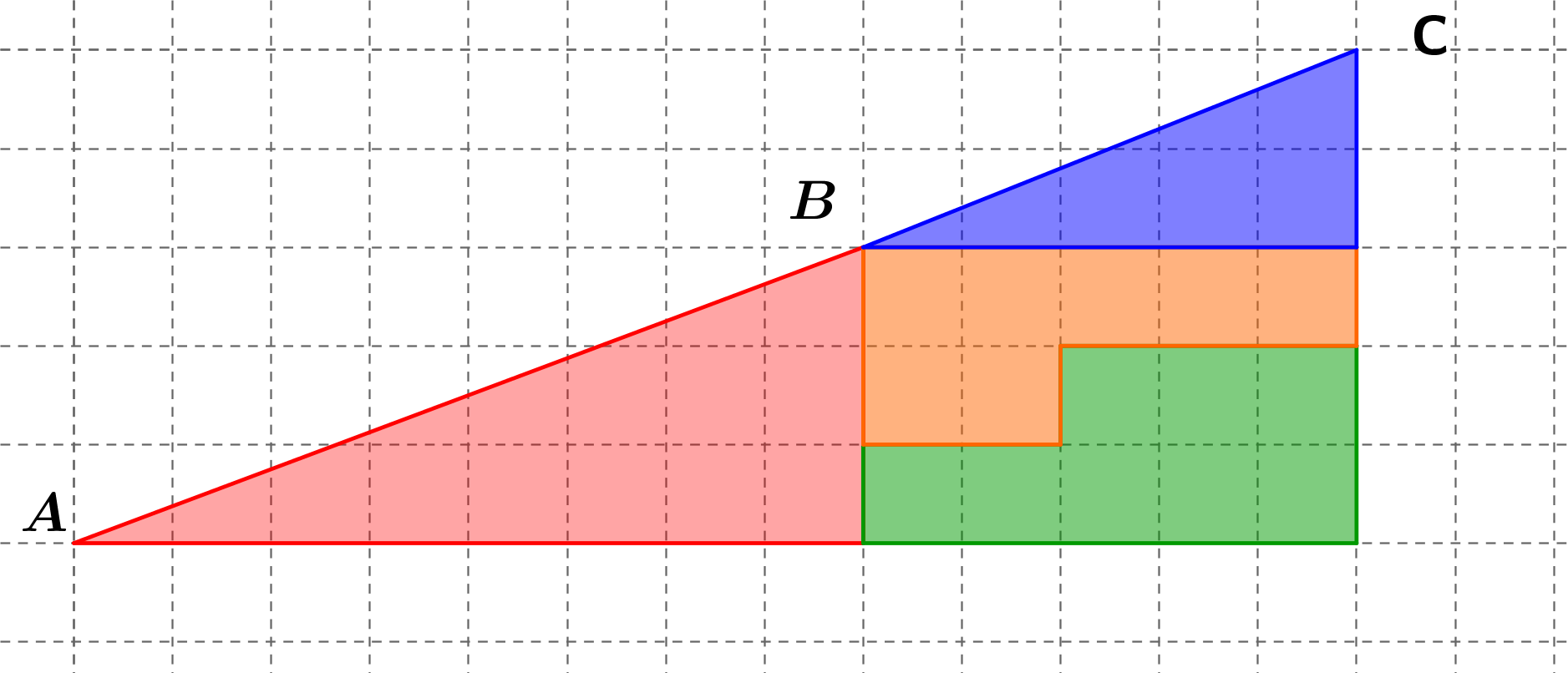
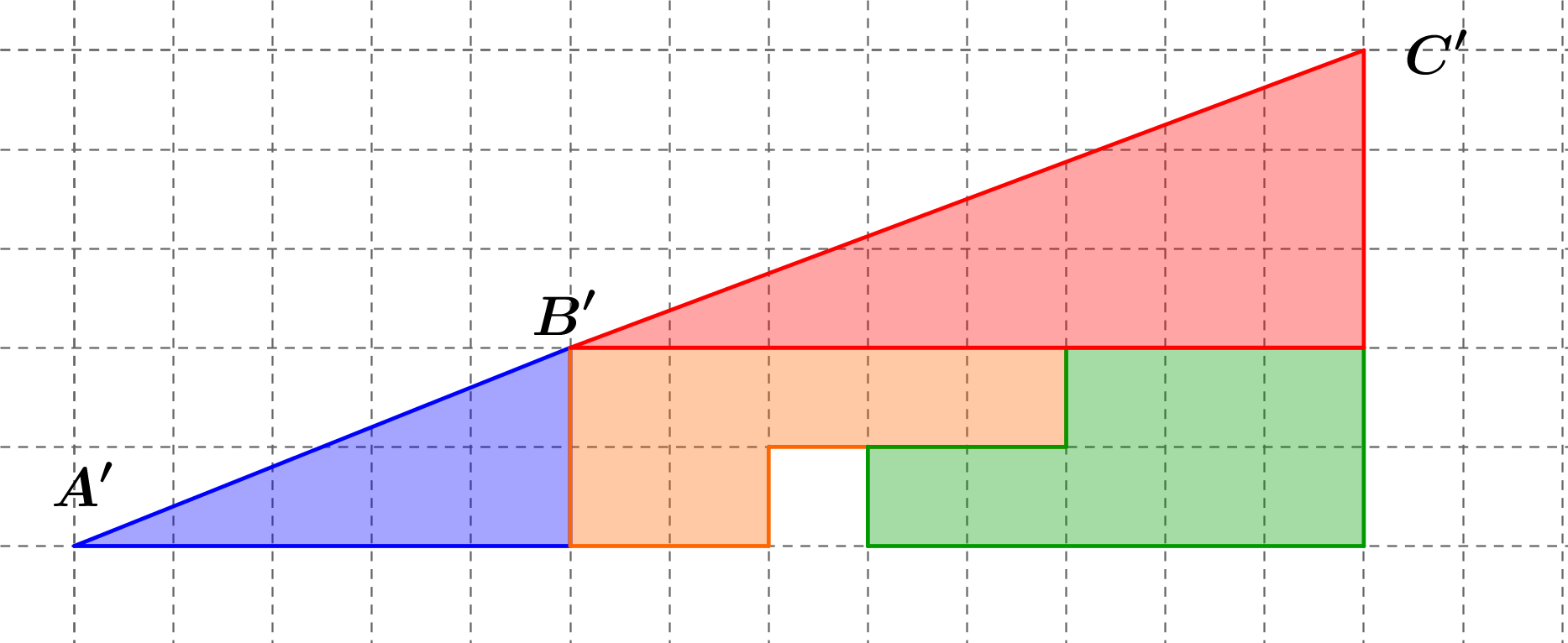


1
Quel problème constate-t-on au niveau des aires ?
2
Démontrer que les vecteurs \(\vec{AB}\) et \(\vec{BC}\) ne sont pas colinéaires.
3
Expliquer l'observation faite à la question 1.
Exercice 3
Dans un repère, on donne les points \(A (1;-1)\), \(B (4;2)\), \(C (-2;5)\). Soit \(D\) le point tel que \(\vec{CD} = \frac{1}{3} \vec{BA} + \frac{2}{3} \vec{CA}\)
1
Faire une figure.
2
On écrit les coordonnées de \(D (x_D;y_D)\). En calculant les coordonnées de \(\vec{CD}\) et \(\frac{1}{3} \vec{BA} + \frac{2}{3} \vec{CA}\), déterminer les coordonnées de \(D\).
3
Emettre une conjecture pour les droites \((AD)\) et \((BC)\) puis la démontrer.
Exercice 4
Soient \(A,B,C\) trois points format un triangle quelconque. Soient \(M\) et \(N\) tels que : $$ \vec{AM} = 3 \vec{AB} \text{ et } \vec{AN} = 3 \vec{AC} $$
\(I\) est le milieu du segment \([MN]\) et \(J\) est le milieu du segment \([BC]\).
En utilisant la méthode de votre choix, démontrez que les points \(A\), \(I\) et \(J\) sont alignés (on pourra se placer dans un repère bien choisi parmi les points donnés, ou utiliser la relation de Chasles).